Google AI developed a deep learning language model called Minerva which could solve mathematical quantitative problems using step-by-step reasoning.
In the recently published paper related to Minerva, researchers explained the development of this deep learning Model. They achieved a state-of-the-art solution by training a deep learning model on a large training dataset that contains quantitative reasoning with symbolic expressions. The final model, Minerva, could solve quantitative mathematical problems on STEM reasoning tasks.
Minerva parses the question using natural language processing and mathematical notation processing techniques. It recalls the relevant formulas, constants, and step-by-step solutions involving numerical calculation. It generates solutions that include symbolic manipulation and numerical computation without relying on a calculator to get the final answers. By generating different answers for the problem with different assigned probabilities, Minerva used majority voting to select the final answer. The following picture shows a sample of Minerva’s output for a quantitative mathematical problem.

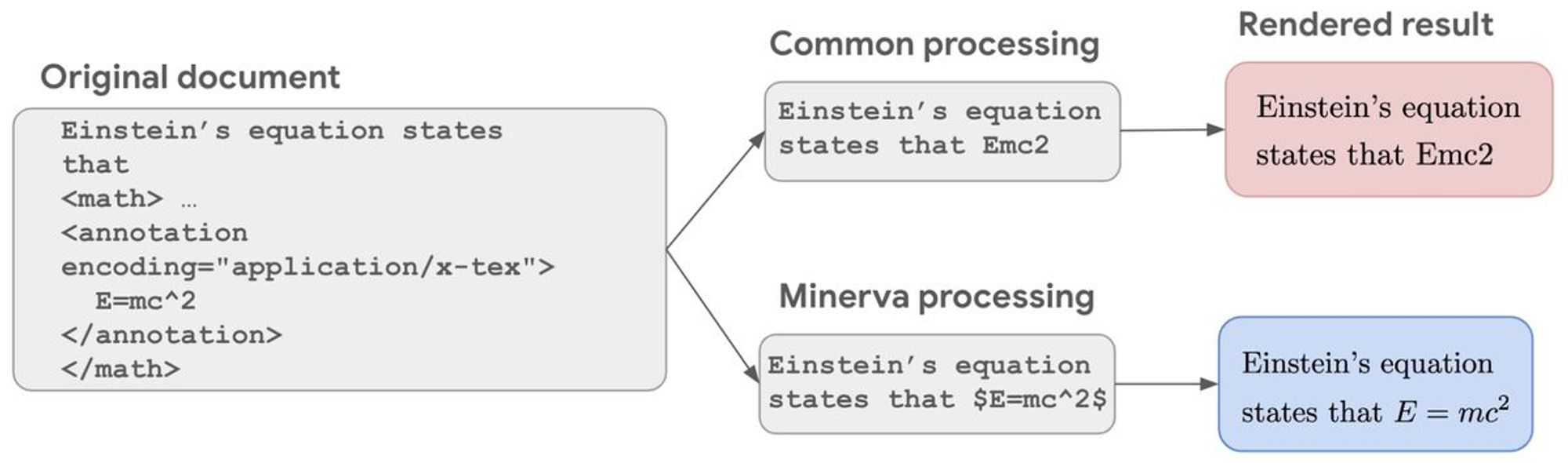
Minerva was built on the Pathways Language Model (PaLM, 540-billion parameter, densely activated, transformer language model) with more mathematical datasets like arXiv, text containing LaTeX and MathJax, or other mathematical formats. To train the model on symbolic data, symbolic mathematical notations are preserved in the training dataset. This process is shown in the following diagram.
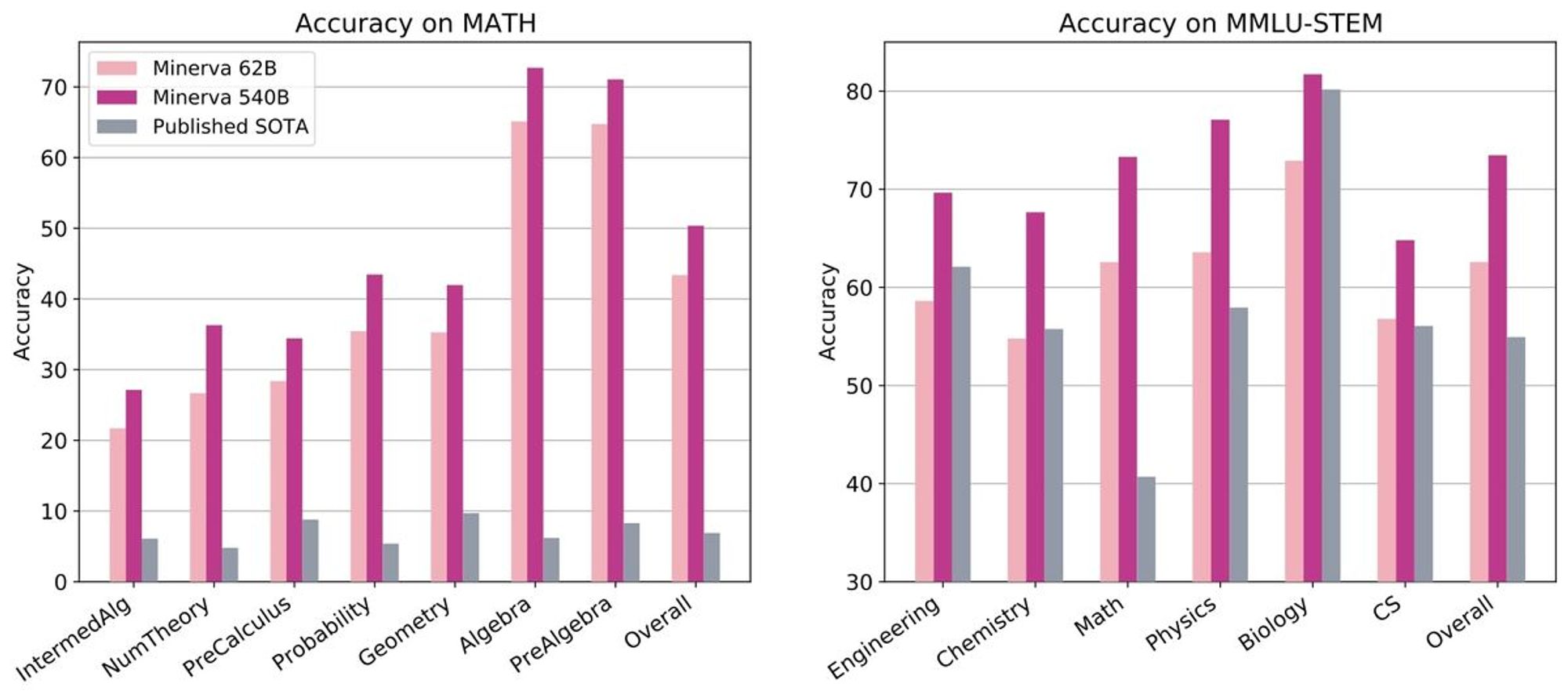
To benchmark Minerva’s performance, STEM benchmarks ranging from grade school level to graduate level were used. Researchers used datasets like MATH (High school math competition level problems), MMLU-STEM (massive multitask language understanding benchmark focused on STEM, covering topics like engineering, chemistry, math, and physics at high school and college level), and GSM8k (grade school math problems involving basic arithmetic operations solvable by a talented middle school student). It shows significant performance on MATH and MMLU-STEM as it is shown in the following graphs:
One of the important limitations of Minerva is that the model’s answers could not be evaluated automatically. As it is stated in the blog post :
Our approach to quantitative reasoning is not grounded in formal mathematics. Minerva parses questions and generates answers using a mix of natural language and LaTeX mathematical expressions, with no explicit underlying mathematical structure. This approach has an important limitation, in that the model’s answers cannot be automatically verified. Even when the final answer is known and can be verified, the model can arrive at a correct final answer using incorrect reasoning steps, which cannot be automatically detected. This limitation is not present in formal methods for theorem proving (e.g., see Coq, Isabelle, HOL, Lean, Metamath, and Mizar).
To evangelize NLP models for quantitative reasoning, Google AI shared an interactive sample explorer for the public to explore Minerva’s capabilities.
Using natural language processing and deep learning in mathematical reasoning is a challenging research area. There are other papers with the source codes in this area like the graph to tree learning, Goal-Driven Tree-Structured Neural Model for Math Word Problems. Paper with code also has some other papers with source code in this domain for further reading.
Inspired by this content? Write for InfoQ.
Becoming an editor for InfoQ was one of the best decisions of my career. It has challenged me and helped me grow in so many ways. We'd love to have more people join our team.